Blog entry: Improving the performance of Nektar++ with SIMD

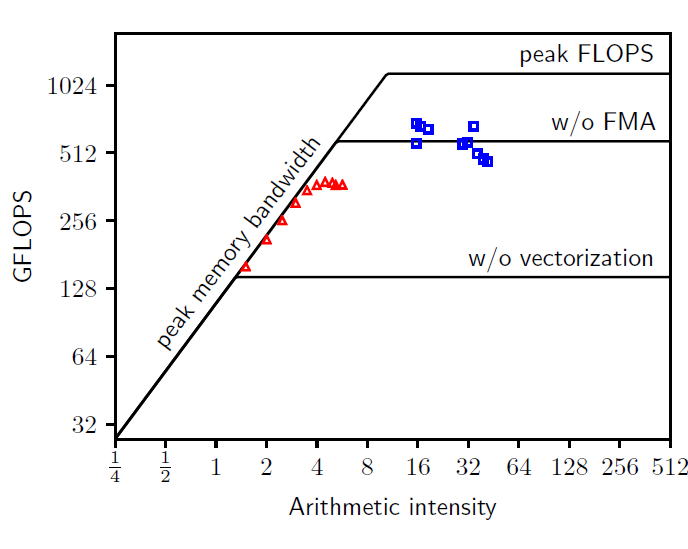
In modern computer architectures, the gap between processor clock speed and memory bandwidth is constantly increasing, meaning that to attain optimal performance, algorithms with a high degree of arithmetic intensity – i.e the ratio between computations performed and the amount of data transferred from the memory (DRAM) – are required. In this context, high-order finite element methods are particularly attractive due to their high (and tunable) arithmetic intensity. Nektar++ is a finite element package designed to allow one to construct efficient classical low polynomial order h-type solvers (where h is the size of the finite element) as well as higher p-order piecewise polynomial solvers. The Nektar++ library comes with a number of solvers and also allows one to construct a variety of new ones. The main solvers provided are a continuous Galerkin incompressible Navier-Stokes solver and a discontinuous Galerkin compressible Navier-Stokes solver. These solvers are routinely applied to industrially relevant simulations; typical applications encompass external aerodynamics (for instance the flow around cars) as well as internal aerodynamics (for instance the flow in aircraft engines). The use single-instruction multiple-data (SIMD) vectorization, that is prevalent on modern hardware, is a well-studied solution for the efficient implementation of high-order operators. We are in the process of integrating within the Nektar++ library some operators (which are based on the work of Moxey et al., 2020) that take advantage SIMD hardware. The intent is to improve the efficiency of the Nektar++ library with the specific end goal of accelerating the compressible flow solver. Figure Caption: Roofline analysis for the vectorized Helmholtz operator (Moxey et al., 2020) on Broadwell CPU using deformed hexadral (triangle) and undeformed hexahedral (squares) elements with varying polynomial order (1-20).

Figure Caption: Roofline analysis for the vectorized Helmholtz operator (Moxey et al., 2020) on Broadwell CPU using deformed hexadral (triangle) and undeformed hexahedral (squares) elements with varying polynomial order (1-20). The roofline analysis is a visual performance model that offers insight to improve algorithms on modern architectures, for instance it can indicate if the computation is memory or compute bound.